Leader Election in Distributed Systems - Notes
Summary of algorithms from the following books:
Synchronous networks
The processing elements (let’s call them processes) form a directed graph. Each node knows the incoming and outgoing neighbors. The link [ channel ] between any two nodes can hold a single message at any given time. Processes work in lock step. A ‘round’ is applying message generation function and put messages on channel along with getting messages from input and apply state transition and remove from channel.
Ring topology
The directed graph is a ring topology. Each node, i.e. process is having a unique identifier, UID which comes from a set of integers.
LCR algorithm
Each process sends it’s identifier around the ring. If the message received has UID lesser than it’s own , then discard that message. If the UID is greater than it’s own then pass on that message and if the UID is same as it’s own, then it becomes the leader.
The process with the largest UID becomes the leader and the algorithm is guaranteed to stop. There are O(n^2) messages generated, as each node generates the message and also passes on it’s own messages.
HS algorithm
The aim is to reduce the number of messages needed to reach to leader election. This assumes a bidirectional graph.
There are phases to this algorithm. In each phase i, process sends out it’s UID in both directions to neighbors that are 2^i distance away. Then it waits for those many hops for the messages to arrive. If both the tokens arrive back, it proceeds to the next phase. If the process gets it’s own UID in the outbound direction, then it is the leader. If one or neither of the tokens arrive, the process drops out as there are processes with a greater UID out there.
Time slice algorithm
Assume that there is a ring with n nodes. In each phase there are n rounds. In each phase i - only the node with UID i can send the message. As a result the first message is sent by the minimum UID. This message travels n nodes and this is the leader message. Inefficient time wise, but would work for small rings with set of UIDs having small numbers.
Variable speeds algorithm
Each process sends message. Message originating from process i progresses 1 step for every 2^i rounds. If a token reaches it’s originator, that process becomes the leader. This guarantees that the second least UID will traverse at max half the distance than that of the smallest UID.
Ring algorithm
This algorithm is similar to LCR, however, there is just one node that identifies a failed leader sending the message to it’s next live neighbor with it’s UID. This node appends it’s own UID to the message set and sends it across. When the payload with set of messages arrives at the originating node, it identifies the process with the largest UID and sends that as the leader messages over the ring. Note that LCR is more optimized in terms of the payload size.
Image source: Database internals by Alex Petrov
Mesh topology
In this topology, each nodes can be connected to multiple other nodes and it’s not necessarily a ring topology. The assumption in some of these algorithms is that the nodes are aware of the diam - which is the maximum distance that exists between any two nodes.
Flood max algorithm
In this algorithm, following assumptions are made:
Each nodes knows the diam
Nodes communicate in bidirectional fashion
Each nodes knows it’s immediate connected node
Each node need not be aware of the entire graph
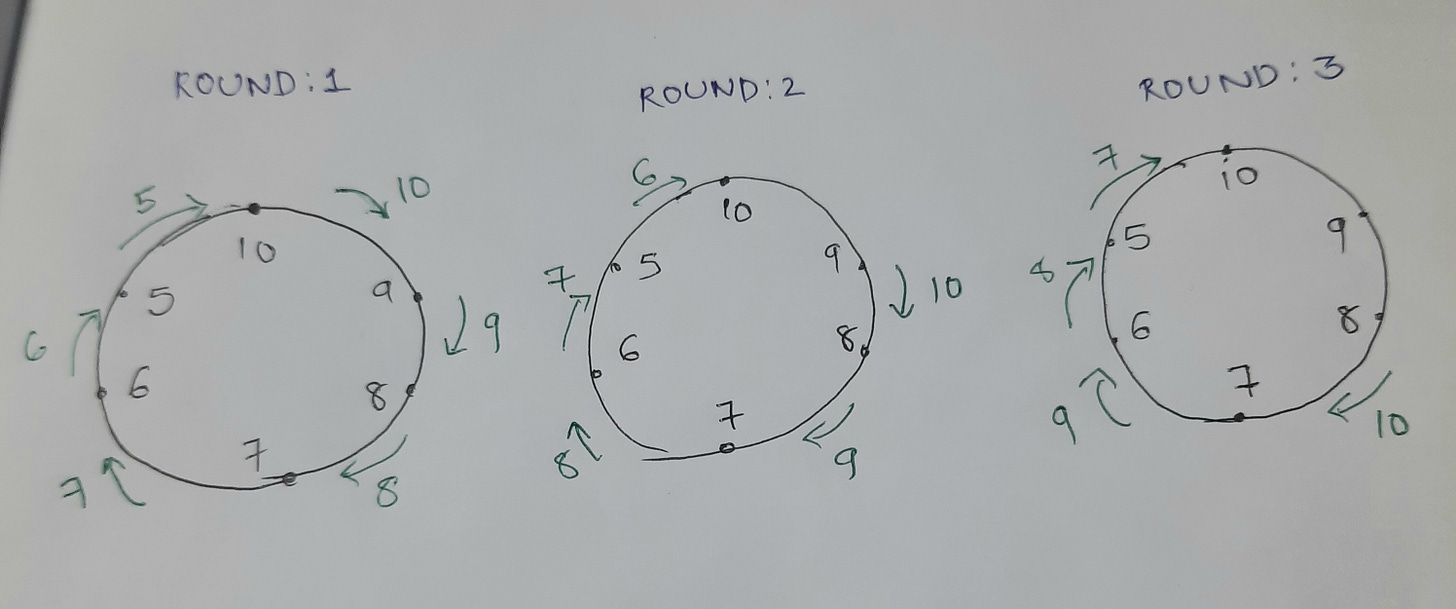
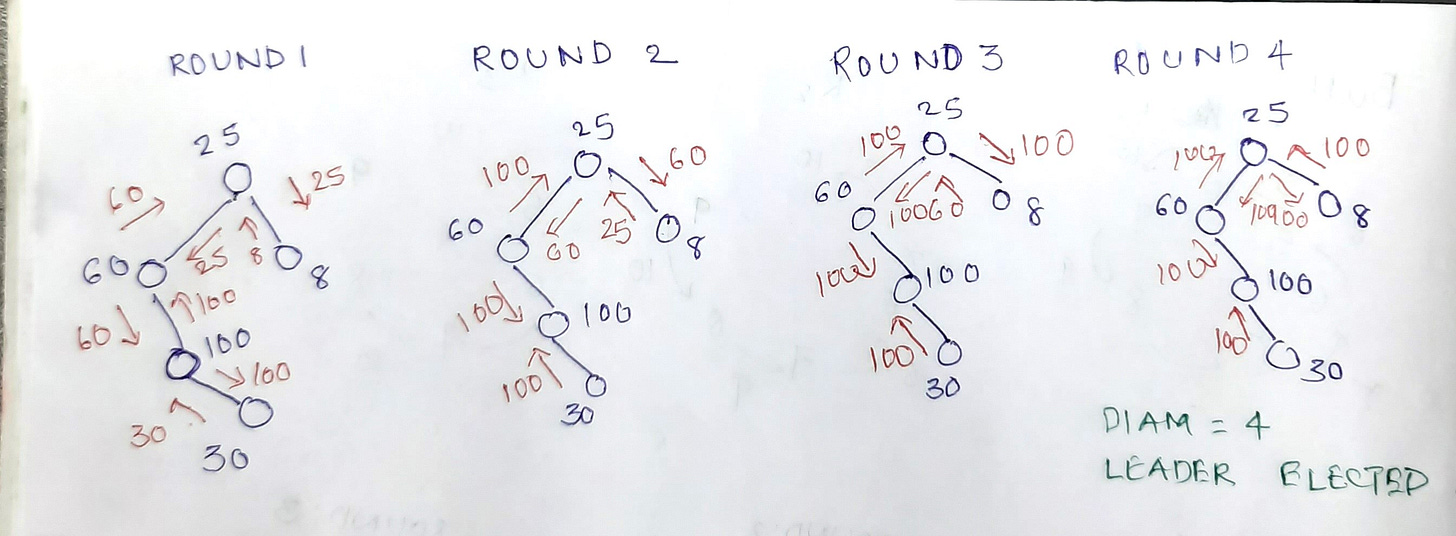
The algorithm takes place in rounds. In each round a node sends the highest UID it has seen thus far to it’s immediate connected nodes. The algorithm starts with each node sending it’s own UID. The nodes that gets back it’s own UID at the end of diam rounds is the leader.
Consider the example below
Note that there could be optimization in terms of the number messages sent. For instance:
Message with the UID of the immediate neighbor is not sent back to the neighbor. So in the example above, in round 2 - node 30 could just drop the message, same with node 60 sending message to node 100, node 25 sending message to node 60 and node 8 sending the message to node 25
If a message with a given UID is already sent to the neighbor in previous round, no need to send the same message in the subsequent round. So in the example above, in round 3 - node 60 need not send message to node 25
Bully algorithm
In this topology, each node is connected to every other node. Each node is also aware of the rank ( let’s assume rank is same as UID ) of every other node.
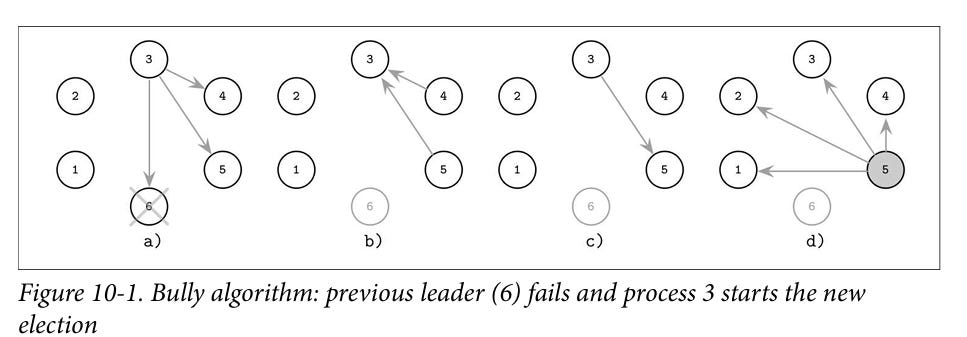
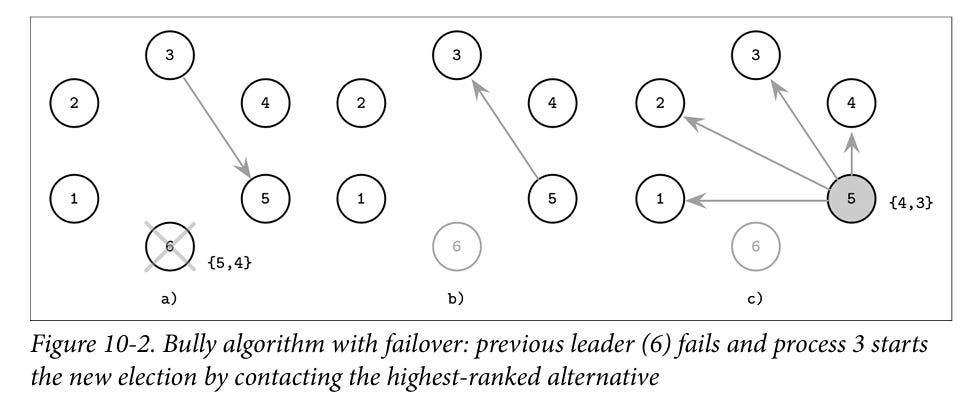
Leader election begins when a node fails to contact a leader or when the mesh is being initialized. The node initiating the leader probe, contacts all other nodes that have the UIDs higher than it’s own. The response from the largest UID is communicated as the leader to nodes with UID smaller than the current node. If the current nodes does not get any response from any of the nodes that have larger UIDs, then the current node declares itself as the leader
Image source: Database internals by Alex Petrov
A variant of the bully is the Next in line failover. Here along with the leader, each nodes also know which would be the next leader in case the current leader fails [ designated survivor] . Hence on leader failure, the probe is sent only to the designated survivor node and the remainder of the algorithm is similar to bully.
Image source: Database internals by Alex Petrov
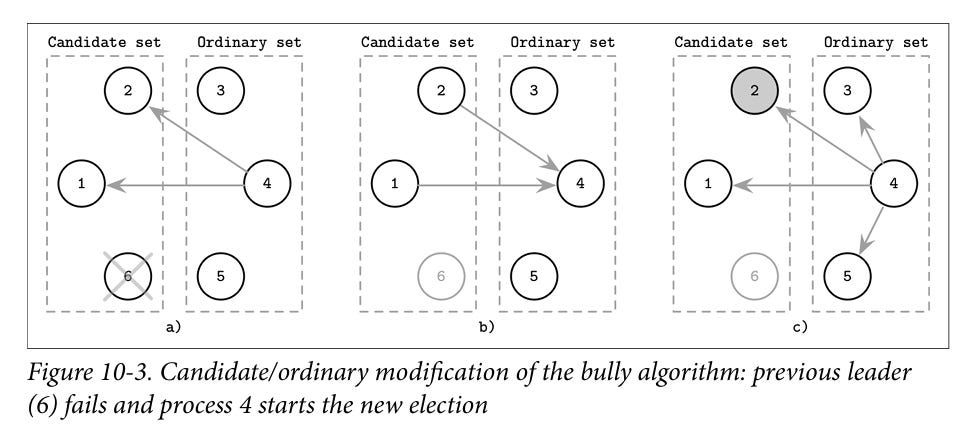
Another variant is the Candidate/Ordinary set algorithm. Here the nodes are divided into two sets: candidate set has set of nodes that can become leaders, ordinary set contains all other nodes. In case of leader failure, the prober process from the ordinary set sends messages to all live nodes from the candidate set. The response with the highest UID becomes the leader.
Image source: Database internals by Alex Petrov
Invitation algorithm
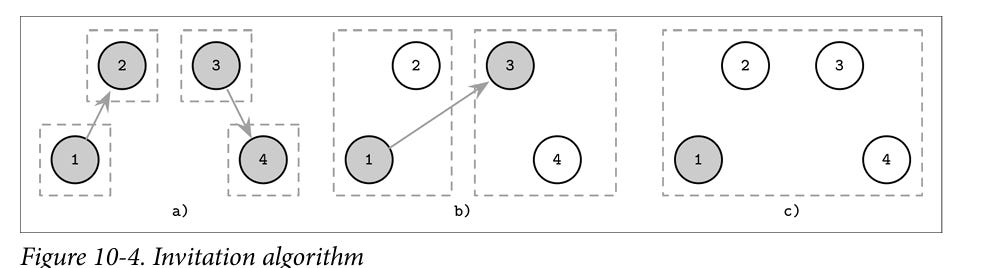
This is a lot like the union-find algorithm. It could also be viewed as a good way to initialize the network to elect the first leader. Each node is initially the leader. Then it contacts subsequent nodes to join it’s group, if the contacted node is also a leader, then the groups are merged, else the leader of the group is contacted. Eventually there is just one elected leader.
Image source: Database internals by Alex Petrov
Asynchronous networks
The primary difference between async and synch networks is that there is no lock step processing in async networks. This means that processes can take arbitrary times to read a message. The communication channel between two nodes is thus modelled as a FIFO queue so that it can hold multiple messages while the receiver is waiting to pick then up.
Ring topology
LCR algorithm
The LCR algorithm that works in the synch network can be extended to work in async network, simply by using the FIFO queue between the processes to hold messages.
The algorithm eventually terminates and elects the process with highest UID as the leader, however there is a time skew and this could take arbitrary long.
HS algorithm
As with the LCR, HS can also be extended to work with the async networks by modelling the communication channel as a FIFO queue. However, since the messages need to travel in both directions, there would be two such FIFO queues.
Peterson algorithm
This algorithm gives O(nlogn) message complexity with unidirectional communication.
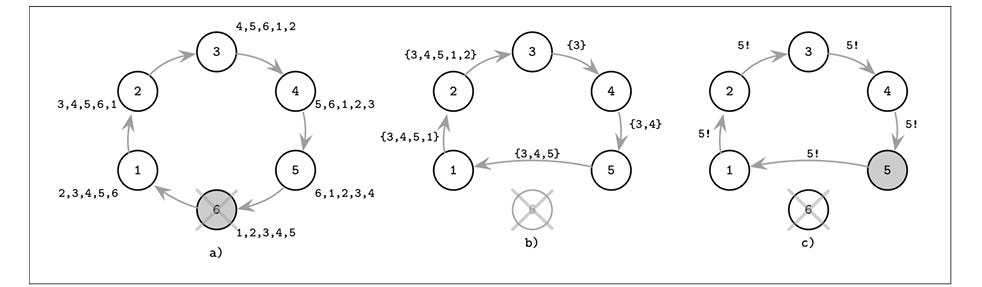
Each process is either in active or relay mode. In the relay mode, the process just forwards messages. In active mode, the process sends it’s UID to it’s immediate two neighbors in the clockwise direction.
Then it checks the messages received from it’s counter clockwise neighbors. If the UID of the immediate counter clockwise neighbor is the largest among the three, the process designates this UID as a temporary UID and remains active. Else the process becomes a relay.
Each active process sends this TUID message over the ring and the active process that gets back this TUID message becomes the leader.
The algorithm starts with each process being in an active state.
Note that this means a process with an arbitrary UID could become a leader.
Below is an example:
Mesh topology
Flood Max algorithm
The flood max can be extended to async networks as well. Here also, the diam is known to all the nodes and to simulate bi-directional communication, we can use dual FIFO queues.
Summary
This is an AI generated summary of the algorithms discussed.